
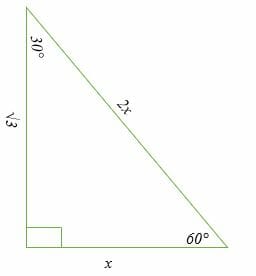
But, this level of trigonometry is done without a calculator. When using a calculator, rationalizing the denominator isn’t necessary. We can say that for an isosceles right triangle, the hypotenuse is equal to the leg times the square root of two. In either case, they’re equal to, “one divided by the square root of two.” Now, with trigonometry we use special notation to signify these ratios. So, the leg : hypotenuse is the same for the triangle with sides of 8 and the triangle with the sides of 19. That means the ratio of the sides is the same. No matter the size of the triangle, if it an isosceles right triangle, it is similar to both of these. What would happen if this triangle didn’t have sides of 8 (unknown units), and instead had sides of 19? So, it is easier to write 2 × 64, than it is to write 128, and then factor it. When simplifying a square root we want to factor to find the largest square number. The reason we do not multiply 2 and 64 is because our next step is to take the square root. (Keep in mind that because it is isosceles, the two legs are the same length as are the two angles, both 45°.) Let’s apply the Pythagorean Theorem to this triangle and see what happens. Our first triangle is the isosceles right triangle. As such, these are about as important to understanding trigonometry as anything other than the fundamentals and basics of what trigonometry is. Their values can be calculated without use of ugly tables, or the use of calculators. While trigonometry can be used for any sides triangle, or any angle for that matter, these two triangles make the foundation. For now, our goal is to really know and understand these two right triangles, inside and out. There are some conventions (or rules) that guide how these triangles are positioned on a coordinate plane, but we’ll get into that in the next section.
It would be a lot of information to memorize, but if understood, is easily recalled.Īll of the values in the table come from repositioning two triangles on a coordinate plane.

Our goal with this section is to learn about where all of those values originate. Just like multiplication is a short-cut for repeated addition and we have tables of values that show us multiplication values (times tables), similar tables of values exist for trigonometry.


 0 kommentar(er)
0 kommentar(er)
